Birçoğumuz fizik biliminin ne kadar zor olduğunu biliyoruzdur. Bazılarımızın akademik hayatında korkulu rüya gibi gözükse de yaşamımızda yokluğu kabul edilemez olağanüstü bir bilimdir. Fiziğin bu kadar dehşet zorlukta olmasının sebebi belki de matematiktir. Lisedeki ilk fizik dersimizde hocamız şunları söylemişti: "…ve şu kanıya varıyoruz. Matematik, fiziğin dilidir ki matematik de fizik kadar zordur. Bunun üzerine bilim adamları fizik biliminin anlaşılması için matematiği aradan çıkarmışlardır. Aradaki boşluğu çeşitli örneklerle doldurup anlamayı kolaylaştırmak istemişler". Bu yazımda sizlere bilincimiz zor kabullenebileceği kuantum süperpozisyon teorisinden bahsedeceğim.   

Süperpozisyon

Adından anlaşılacağı üzere süperpozisyon, çeşitli pozisyonların durumunun süper (Birden fazla) durumda olmasıyla ilgilidir. İlk olarak 1750’li yıllarda Daniel Bernoulli tarafından ortaya atıldı. İlke belirli dönem çeşitli bilim adamları tarafından reddedilmiştir. Daha sonrasında Joseph Fourier’in çalışmaları sonucunda kabul görmeye başlamıştır. Daha sonrasında Schrödinger denklemleriyle kuantum fiziği açısından ne kadar önemli olduğu ortaya konmuştur. 

Süperpozisyonu olduğu gibi anlayabilmek için ileri düzey matematiksel analizleri çok iyi bilmek gerekir. Tabi bu durum, diğer fiziksel hâller için de geçerlidir. Zaten fiziğin bir diğer zor yanı da, onu matematiği kullanmadan aktarmaya çalışmaktır. Bir önceki yazıda Schrödeinger’in kedisinden bahsetmiştim. Orada radyoaktif atomun üst üste binme durumu -yani süperpozisyon- söz konusuydu. Orada anlatılanlara bakıldığında süperpozisyonu çok soyut bir olgu olarak algılamış olabilirsiniz. Ancak bu durum hiç de öyle değildir. Süperpozisyon hayatımızın her alanında mevcut, anlaşılması gayet kolay bir olgudur. 

Fourier Analizi

Kuantum süperpozisyonun birçok bilimadamı tarafından yapılan reddine Fourier yaptığı çalışmalarla karşı durmuştur. Metal bir çubuğun farklı sıcaklıklardaki iki yüzeyinin sıcaklık dağılımını hesaplamak için Fourier çalışmalar yapmıştı. İki farklı yüzey, farklı sıcaklıkta -yani farklı frekanslarda- ışıma yapmaktadır. Bunlar ayrıca birbirinden farklı fonksiyonlardır. Fourier bu birbirinden farklı fonksiyonların değişik frekanslarının dik toplamını hesapladı. Bu hesaplamalar geometrik açılarla bağıntılı olduğu için sinüs ve kosinüs fonksiyonlarını kullandı. Günümüz matematikçileri bu trigonometrik fonksiyonları Eulier bağıntısı ile yazdılar. Bunun sonucunda da fonksiyonlar kompleks üslü sayılarla gösterildi. Bu gösterime Fourier serisi denir. Bu seri birden fazla fonksiyonun frekansının kolaylıkla toplanmasını sağlar. Yani birden fazla girdi fonksiyonunun çıktısını daha kolay bir şekilde elde edebiliyoruz. İleride süperpozisyonun yorumu ve matematiksel izahından bahsedince Fourier analizi ile ilişkisini anlayacaksınız. 

Çift Yarık (Young) Deneyi

Daha önceki yazılarımda çift yarık veya Young deneyinden bahsetmiştim. Bu deney süperpozisyonu anlamak için çok önemli bir örnektir. Lise yıllarımızda bu deneyin klasik fizikle ilgili olduğunu zannederdik. Ancak bu deney maddelerin kuantum durumlarının belirlenmesinde çok önemliydi.

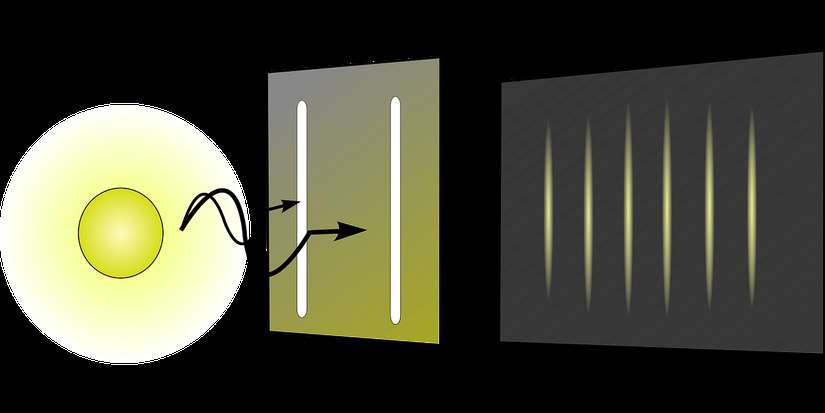
1803 yılında Thomas Young, maddenin doğasındaki ikiliği ortaya koymak için ilk çalışmalara başladı. İlk olarak noktasal bir ışık kaynağını, üzerinde tek yarık olan bir engelin merkezinin uzağına yerleştirdi. Engelin arkasına da ışığı yansıtabilen bir perde astı. Deneyi çalıştırdığında kaynaktan çıkan ışınlar yarıktan geçerek perdede tek bir ışık çizgisi oluşturdu. Daha sonra engelde var olan yarık çizgisine paralel bir yarık daha açtı. Bu sefer kaynağı çalıştırdığında perde üzerinde iki adet ışık çizgisi olmasını bekledi. Ancak kaynaktan çıkan ışınlar birbirleriyle girişim ve kırınım yaptı ve perde üzerinde çok sayıda girişim deseni oluştu. Bu durum bize ışığın veya fotonun dalga özelliğini göstermektedir. Ancak ölçümler yapıldığında fotonların dalga değil, tanecik özelliği gösterdiği sonucu ortaya çıkıyor. Bunun üzerine birçok çalışma yapıldı ve fotonlarla ilgili yazımda da belirttiğim gibi dalga-parçacık ikiliği keşfedildi.   

Sonuç hep paradoks

Bilim adamları çift yarık deneyindeki birden fazla girişim desenini, fotonların dalga özelliğine bağlamıştı. Aynı zamanda tanecik özelliğinden dolayı, taneciklerin birbirini itme durumu da söz konusuydu. Bunun üzerine bu deneyi bir de elektronlarla yapmaya karar verdiler. Deneyin tüm aşamalarını aynen uyguladıklarında sürekli aynı sonuçlar elde ediyorlardı. Ancak tek bir elektron, çift yarığa gönderildiğinde ne olacağını merak ettiler. Aslında tek bir parçacık hâlinde elektron, girişim deseni oluşturamaz. Çünkü birbirini ittirecek elektronlar olmadığından tek bir elektron girişim deseni yapmaya yeterli olmayacaktır. Ancak sonuçlar hiç de bekledikleri gibi olmadı. Tek bir elektron gönderdiklerinde bile çift yarıklı engelin arkasında yine girişim deseni oluştu. Çift çizgi değil, girişim deseni… Demek ki tek bir elektron, nasıl oluyorsa dalga özelliği gösterebiliyordu. Gözlemlerimiz bizlere elektron veya foton hiç fark etmeksizin dalga özelliğini göstermektedir. Ancak bu deneyi ölçümlerle test ettiğimizde her türlü tanecik özelliği karşımıza çıkıyor. Sanki ikisi beraber gibi ama ölçümler öyle olmadığını söylüyor. Tamamen sağduyumuza ters!

Girdiler ve çıktılar

Kuantum süperpozisyonun matematiksel izahı çok karmaşıktır. Ancak matematiksel izahını anladığınız zaman bu teori sağduyunuza daha da yatacaktır. Bunun için de matematiksel izahı olabilecek en dibe indirgeyip basit işlemlerle aktarmak en uygun yol olacaktır. 

Elimizde iki kutu olsun. Kutularımızın ismi “X” ve “Y” olsun. Bu “X” ve “Y” kutularının içlerinde de “A” ve “B” nesneleri olsun. Bu nesneler aslında birer vektördür. Ancak bu “A” ve “B”den hangisinin hangi kutuda olduğunu bilmiyoruz. Şimdi rastgele bir kutu seçelim. Bu kutunun içerisinde hangi nesnenin olacağını kesin olarak bilmiyoruz. İki nesneden sadece biri çıkabilir. Bu da %50 olasılık demek. Aynı durum diğer kutu için de geçerlidir. Fakat “A” veya “B”den biri kutuların ikisinden birinde bulunacağından olasılık olarak ikisinde de bulunabilir. Yani bir kutu içerisinde iki nesne de olasılık olarak var ama kutuyu açıp baktığımızda sadece bir tanesi çıkacak. Tıpkı Schrödinger’in kendisindeki gibi... Matematiksel fonksiyon olarak kutuları girdi, nesneleri de çıktı olarak ele alalım. “X” girdi kutusundan “A” çıktı nesnesi, “Y” girdi kutusundan da “B” çıktı nesnesi vardır. Fourier analizindedir gibi her iki bağıntı da birer fonksiyondur. Ve bu fonksiyonlar toplanırsa (X+Y) girdi kutularından (A+B) çıktı nesneleri alınır. 

Girdi:X > Çıktı:A %50

GirdiY > Çıktı:B %50

Toplam Sonuç= Girdi: X+Y > Çıktı:A+B %100

Hilesiz bir zarı attığımızda üst yüze gelen sayının tek veya çift olacağını biliyoruz. Atmadan önce üst yüze gelecek sayı tek veya çifttir ve birbirleriyle yarış halindedir. İkisi de gelebilir. Kuantuma göre her ikisi de zar atılmadan önce birbirleriyle üst üste biner ve ikisi de gerçekleşir. Ama gözlemler sonucunda yalnızca biri gerçekleşir. İşte altı ay sonunda bu paradoks sonucuna ulaştım.

Yazılım Mühendisliği Öğrencisi

Kuantumla ilgili birçok olgu sağduyumuza terstir. Bunlardan biri de kuantum süperpozisyon teorisiydi ki hâlâ bu teori üzerinde çalışılmakta. Belki bu yazıdan sonra aklınız iyice karışmış olabilir. Belki birkaç cümleyi, defalarca okumanız bile gerekti. Ama merak etmeyin, bilim adamları bile bu teoremleri ancak integrasyon ve mertebeli diferansiyel gibi kavramlarla algılayabilmektedir.